Notes on Dimensional Analysis

发表于 更新于 阅读次数： Waline：
✨一个可能没什么用的量纲分析（以及其他？）笔记。

Foreword

​ 大三量子力学时，学到许多神奇的数学物理操作技巧。其间在推导谐振子无量纲形式方程时，发现了自然单位制的神奇力量，就此挖下量纲分析大坑。大四听重整化群课程时，相关内容如标度变换等等，也与量纲分析有关。研一 DFT 课程开篇又介绍了原子单位制以及与量纲有关的简化方法，令人回忆起两年前看到简洁的无量纲方程时产生的 “还能这样？” 的神奇体会。大坑一拖两年有余，终于在寒假旅游摸鱼期间，零碎整理于此。

（完全没搞懂）

主要内容参考:

  • Mathematical Analysis of Problems in the Natural Sciences ( Zorich, 2008 )

  • 《定性与半定量物理学》 （第二版）（赵凯华，2017）

  • 相变与重整化群 课程笔记，授课老师：同宁华教授（2020 年秋季，于北理工）

  • LECTURES ON PHASE TRANSITIONS AND THE RENORMALIZATION GROUP ( Goldenfeld, 1992)

量纲分析-理论基础

​ 量纲分析（Dimensional Analysis）的概念最早由 Joseph Fourier 于 1822 年提出。这一方法通过研究不同物理量的基本组成量（例如长度，质量，时间，电流等）及其单位（例如：英里与千米，英镑与千克，等等）的关系来简化实际问题。具有相同量纲的物理量（Commensurable physical quantities）之间可以比较大小，即使具有不同单位。但在具有不同量纲的物理量（Incommensurable physical quantities）之间比较大小是没有意义的。

​ 量纲分析理论中的基本假设是 比值绝对性假设（Postulate of the Absoluteness of Ratios） 。例如，有两个具有相同量纲的物理量

其中 和 是具有相同量纲的 个自变量，比如 边形的各个边长。那么比值绝对性假设给出 即在改变基本单位（长度，质量，时间等）的大小时，具有相同量纲的物理量 和 的数值按相同倍数改变，这一倍数仅由物理量的类型决定。

量纲函数和量纲公式

​ 上式指出，两个物理量之间的比例关系只与 有关。亦即 由此能够推断出函数 的形式。首先，注意到 对 求导，再令 ，得到 满足的微分方程 考虑初始条件 后，量纲函数的形式就是 在导出这一结果的过程中，我们始终假设变量 具有相同的量纲，但如果某一个物理量的自变量是几组不同量纲的量，即 其中相同字母标记具有相同量纲的物理量。假设不同的自变量可以独立进行标度变换，那么按照上面的假设，可以得出 其中，数组 称作量纲矢量（dimension vector），函数 称为量纲函数（dimension function）。

​ 如果一个物理量的量纲矢量是零矢量，那么称它是无量纲的（dimensionless）。例如物理量 的量纲函数是 ，那么就有无量纲量

定理

​ 考虑一个一般形式的物理量 ， 其中只有前 个自变量具有独立的量纲。如果做标度变换，令 可以得到无量纲量的关系式 其中 于是物理量 可以写成下面的形式： 这种变换可以减少函数变量的个数，上式这种一般形式的变换关系被称为 -定理。

这一定理的直接应用是工程技术等领域中的相似性原理。人们可以在实验室中利用小模型进行模拟实验，然后根据 -定理进行标度变换，还原出大型飞行器、轮船等物体的实际情况。

例1：证明勾股定理

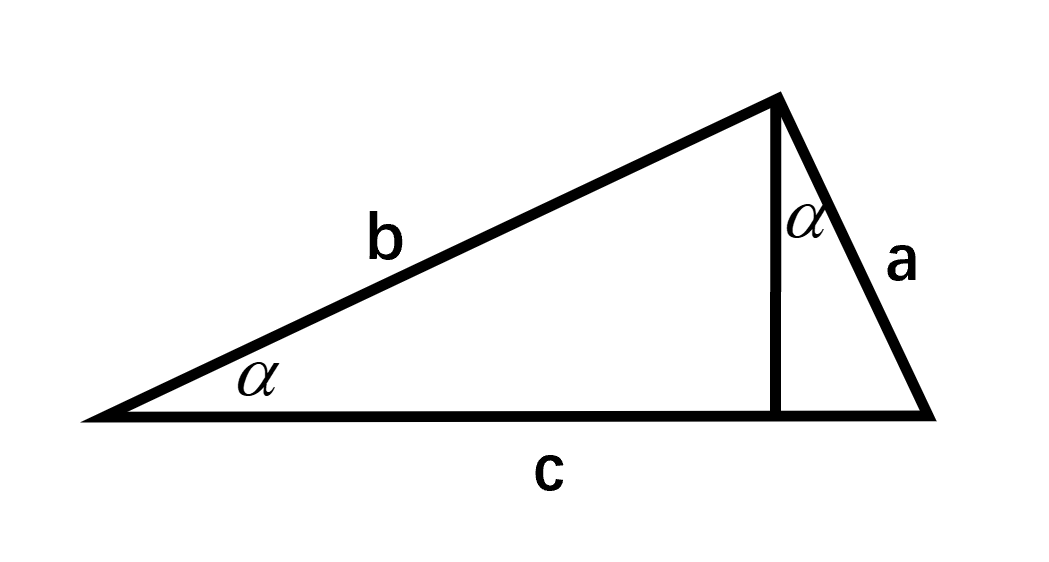
直角三角形勾股定理

一个直角三角形的面积 可以由一个斜边 和一个锐角 唯一确定。由于角度是无量纲的，那么 可以用量纲函数表示为 如图，作垂线将三角形分为两个小直角三角形，它们各自的面积又可以表示成 由于面积 ，有 消去 就得到勾股定理

例2：单摆的周期

​ 质量为 的重物固定在长度为 的轻绳上，初始位置在距离平衡位置 角度处，在引力和绳拉力作用下做单摆运动，可以用量纲分析方法导出单摆运动周期 的比例关系。首先将量纲矢量变换到一般的 单位制下，亦即 从中可以看出，，， 是量纲独立的，而 。那么可以由 -定理得到， 其中 是一个无量纲因子，只与初始角度 有关。这一因子的具体数值可以通过求解单摆的第一类椭圆积分得到（参考朗道《力学》第三章习题1）。

例3：量子真空涨落

（据说是某年 CUSPEA 试题）

​ 两块无限大平行平面壁相距 ，都是理想导体。在经典电磁理论下，两块平板之间没有相互作用。但如果计及相对论性电磁场的真空涨落效应，两平板间单位面积上的作用力（压强） 与距离 之间有怎样的函数关系？

考虑相对论性电磁场，有真空中的光速 ，普朗克常量 ，还有距离 都是 的自变量，即 列出量纲的变换关系表 其中 ， ， 是量纲独立的，而 。所以 真空涨落引起的单位面积吸引力反比于两板间距的四次方。

标度理论与标度关系

​ 在上面的三个例子中，我们可以通过简单的量纲分析得到物理量之间的指数关系。但有一类更宽泛的物理问题，其中会出现指数律关系，但无法导出简单的分数形式的指数。比如在统计物理的相变过程中，临界点附近的函数具有奇异性，指数关系就不具有解析形式，需要用其他方法来考虑指数的具体数值。

齐次函数（Homogeneous Function, HF）

​ 设有单变量函数 ，若对于任意实数 ，有 ，那么称 是齐次函数。

​ 可以证明，只有单一幂次的幂函数是齐次函数。证明如下。

设有任意实数 和 ，那么有 以及 所以 两边对 求导，得到 令 ，得到 再令 ，得到 ，以及 两边对 从 0 到 1 积分，得到 于是得到 的表达式（略去常系数） 所以有 是单一幂次的幂函数。

广义齐次函数（Generalized Homogeneous Function, GHF）

如果多变量函数 对任意实数 ，存在 和 使得 那么称 为广义齐次函数。令 ，得到 于是有 GHF 的一般形式 如果考虑 元 GHF ，对任意 ，应满足 称其中的 为标度幂次（scaling power）。相应的等价形式是 即一般形式的 GHF 其中， 是 元函数。后面可以看到， 这里定义的 scaling power 与相变和重整化群过程中的临界指数有着密切的联系。

Widom 标度理论

以经典铁磁相变（这里的“经典”指的是不考虑热力学涨落）为例，有 其中 是格点数， 是总自由能， 是平均每一个格点的自由能； 是临界温度。

相变发生在 ， 处，因此需要研究在自变量趋于零时，函数中奇异项的变化规律。Widom 标度理论的前提假设是，单位格点的自由能只与 和 有关，并且是广义齐次函数 其中 是奇异项，高阶导数会发散； 是非奇异项，高阶导数不发散。由于所有临界指数的性质都和奇异项有关，在此可以先不考虑非奇异项。

（施工中）