双时推迟(超前)格林函数及其应用
首先对之前课程内容作两处补充.
补充1.
谱函数取实值与算符之间的关系
下面简单讨论一下当 是厄米算符时,
在什么情况下谱函数
会是实数. 我们考虑以下两种情况:
- 和 都不是厄米算符, 但 是厄米算符.
在这种情况下, 算符具有性质 具有这种性质的算符对的例子有 和 等.
谱函数可以表示成 谱函数的厄米共轭: 其中算符矩阵元的乘积具体表示为 以及 因此在这种情况下, 谱函数满足 是实数.
- 如果算符 和 都是厄米算符, 且 , 从而
是厄米算符.
此时考虑算符矩阵元的乘积, 有 因此这种情况下不满足 ,
谱函数不是实数.
综上讨论, 只有当算符 和
都不是厄米算符, 但 是厄米算符时,
谱函数是实数.
补充2. 对自旋波态
的讨论
考虑自旋波态 其中 表示在第
个格点上有自旋偏转的自旋缺陷态(已归一化). 下面讨论自旋波态中,
归一化系数的确定, 以及这一态函数的物理含义.
在自旋波态的本征方程中, 取试探解 代入本征方程, 得到 其中 能够分离变量的系数最简单形式是指数函数, 即满足条件的 是 从而有 前面的常系数
可以利用波恩-卡门边界条件来确定, 即 是倒格矢,
如果限制在第一布里渊区中, 有 其中
是倒点阵基矢. 倒点阵基矢和正点阵基矢之间满足 由归一化条件 得到 从而定下系数 . 所以有归一化后的自旋波态
之所以称其为自旋波态, 是因为
代表一个集体激发的态. 考虑这个态在 方向的自旋分量, 应有 这与基态只差一个自旋量子数, 而它被 个格点分担, 每个格点分担 . 所以这个态应与格点指标 无关. 引入算符 自旋波态可以改写为不带格点指标 的形式 各个格点的自旋沿
方向的投影应当是一样的, 但在
平面上的自旋方向不同. 如果把自旋箭头连起来, 就形成了一个自旋波,
这是一种集体激发. 自旋波所对应的准粒子称为磁振子(magnon). 自旋波态的波长
.
哈密顿量的本征态可以由磁振子的量子数来确定,
自旋波态的能量就对应着磁振子的能量.
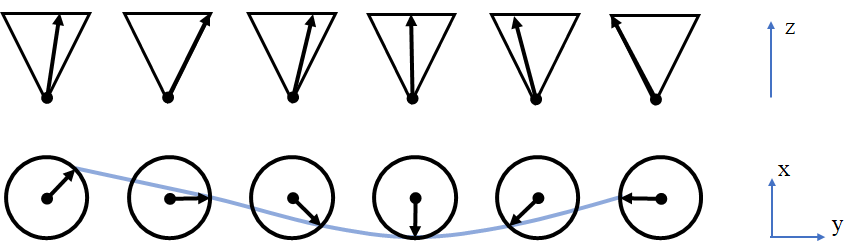 铁磁海森伯模型的自旋波态在 z
方向的投影和在 x-y 平面上的自旋波.
铁磁海森伯模型的自旋波态在 z
方向的投影和在 x-y 平面上的自旋波.
在铁磁自旋波理论中, 哈密顿量 其中 和
是磁振子的产生消灭算符. 所以应有自旋波理论的基态 其中
代表磁振子的真空态. 这一真空态同时也是 H-P 玻色子算符的真空态, 即 此外, 还可以证明, 在 H-P 变换后, 自旋波态可以写成 的形式. 其中, 第二步到第三步按级数展开的形式理解根号下的算符,
展开式中除了零阶项 外,
每一项都带有一个消灭算符
在最右边, 利用 , 就只剩下了零阶项.
再利用变换关系 就得到了
(. . . 续上次)
格林函数方法的实际应用
对铁磁海森伯模型的应用
格林函数方法(考虑)
引入如下格林函数: 再通过傅立叶变换, 就可以计算 . 然后利用谱定理
计算均值.
我们先讨论更一般的情况. 考虑如下双时格林函数: 当温度 时,
格林函数要在基态下求平均值, 即 其中, 由于自旋上升算符 作用在基态 上得零, 因此上式第二项取值为零. 在时间 时, 第一项 上式的物理含义是, 初始在 时刻用 对基态 作用一次, 在格点 上产生一个自旋缺陷, 经过了 时间的演化和传播在 格点上产生缺陷的几率幅.
因此上式相当于一个传播子,
它对时间的傅立叶变换的极点应该能够给出系统元激发的相关结论.
下面利用运动方程法求解这一格林函数.
对时间求导数, 得到 其中,
是一个正无穷小量. 根据对易关系, 上式第一项中的均值可以化简成 运动方程中第三项需要做适当的近似处理, 以使得运动方程闭合.
考虑对易关系: 代入运动方程的第三项, 得到 第三项 为了使上式尽可能地接近格林函数的原始形式, 从而方便求解,
需要作出大胆近似. 1959 年 恰布里科夫(Tyablikov) 提出一种切断近似,
将自旋沿 方向分量 用其平均值 替代.
此外, 由于不同绘景下的力学量平均值相同, 近似处理还可以写成 .
由于格点具有平移对称性, 平均值与指标 无关, 因此还可以略去下标.
作业 10 验证:
经过上述处理, 运动方程可以改写为 为处理最后一项中的 ,
引入对时间的傅立叶变换 将上式代入, 就得到了频率表象下的格林函数运动方程: 考虑到平移不变性, 格林函数 是关于变量 的函数,
于是可以进一步引入空间点阵的傅立叶变换, 有 于是格林函数变成 其中: 是结构因子,
.
根据格林函数的表达式, 是 的极点实值,
考虑其物理意义, 应该与近似处理后系统的激发能有关.
当温度 时, 自旋沿 方向分量应趋于常量, 即 , 因此有
格林函数的傅立叶变换形式为 如果取 ,
就得到与自旋均值相关的格林函数 由此可以得到 其中第二步利用了 这样就得到了算符 平均值的表达式(取 ) 由于
中会有 ,
所以这是一个超越方程. 如果引入一个函数 可以得到形式解 上式在取低温和高温极限后, 可以得到解析解,
在中间温度则需要数值求解. 下面考虑低温区和高温区解的情况.
(i) 低温区()
在低温近似下, 有 这样, 函数 变成
可以作为小量进行展开, 变成
相应地有
方向磁矩可以写成 其中
是固有磁矩的值. 这一结果与前面给出的自旋波理论结果一致,
区别仅在于近似方法不同.
(ii) 高温区 ()
自旋形式解的分母可以用双曲余弦函数写出, 即 利用双曲余弦的展开式 , 得到解的近似形式 其中, 考虑到 再令 超越方程就可以写成 对等式右边分子分母同乘以 ,
得到 可以利用二次式求根公式得到这一方程的解(略去无物理含义的负根),
即 为确定
的值, 利用 , 即 由此解得: 对 取近似, 取括号外的 , 有
作业 11
证明 在三维情况收敛,
而在一维和二维情况下发散.
作业 12
证明在低温区: 在三维情况下收敛, 在一维和二维情况下发散.
(第五讲完.)
