零温单粒子格林函数,
费曼图技术及其应用
费曼图技术在凝胶模型中的应用
密度关联格林函数
回顾前面得到的, 电子间严格的有效相互作用的费曼图是
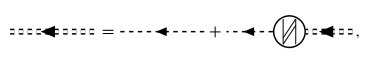 001
001
对应的表达式:
严格的总极化图展开式为
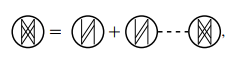 002
002
对应的表达式为
最强发散项近似的有效相互作用表达式为
 003
003
对应的数学表达式为 在这一近似下, 极化图展开为
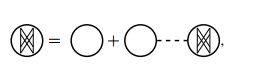 004
004
对应的表达式为 总极化
对应着(因果)密度关联格林函数, 是 Lindhard 函数.
这一形式可以得出与上一章相同的结果.
有效相互作用可以进一步改写成 其中有 称为系统介电函数. 最强发散项近似下有 于是有一般成立的关系式: 下面具体计算在几种极限下的 Lindhard 函数.
(A) 长波极限().
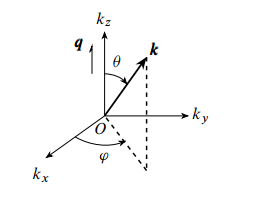
根据之前的计算, 得到 其中 采用球极坐标
 005
005
Lindhard 函数进一步写成 在长波极限下, 取值很小, 相应有 . 取极限 , 只保留到一次项, . 于是积分与 无关. 利用对 的限制:
积分式可以写成 令 , 有 再引入 , 得到 利用柯西主值积分, 第一项: 其中, 当
时, 有 代回第一项积分, 有 类似地, 有第二项 两项合并, 得到 代回 Lindhard 函数中, 有 其中有 , , . 考虑小量展开 有 总极化的表达式 等离激元的振荡频率由上式的极点方程给出, 即 即得等离振荡频率, 也就是系统集体激发的准粒子能谱.
(B) 静电屏蔽().
Lindhard 函数: 其中, 虚部始终为零. 考虑括号中第二项: 作变量代换, 有 , 得到 这里得到的结果, 分子不变, 分母差一负号, 即有 . 于是 表达式中只需要考虑第一项. 有:
其中第二步取 . 再利用积分公式 表达式进一步写成 其中有 . 下面利用这一结果来讨论系统的有效相互作用.
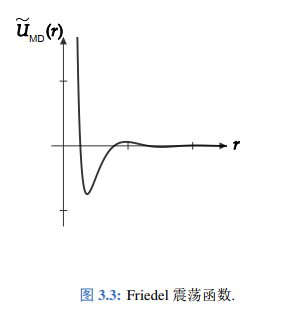
傅里叶变换到实空间下, 有 在
时振荡衰减. 这一结果常称为 Friedel 震荡, 如图所示.
 006
006
下面讨论
的情况:
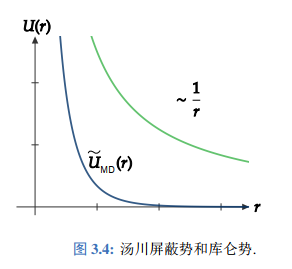
其中有 我们称 为 Thomas-Fermi 屏蔽长度. 并有 称为汤川(Yukawa)屏蔽势, 如图所示.
 007
007
下面讨论一下最强发散项近似的成立条件.
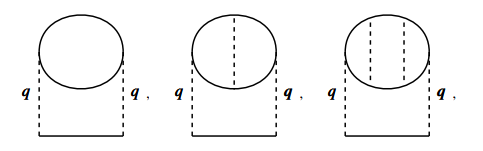
考虑这样三种自能图:
 008
008
这三种图的发散程度相同, 但我们在取近似时, 只考虑了第一种,
而忽略了后两种. 这是因为在高密度情况下, 第一项的贡献要远大于其它项.
下面证明这一结论.
在高密度近似下, 假设一个电子所占据的体积可以用等体积的球来描述, 即有
引入无量纲参数 , 令
, 其中 是氢原子玻尔第一轨道半径, 有 . 高密度近似对应着 , 即 下面主要分析  和
和  的贡献.
的贡献.
(a)
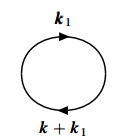
(b)
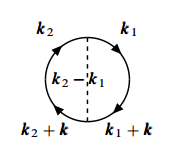 可以看出, 两个表达式的关系为 考虑两个函数的比值, 有 上式在高密度极限下远小于 1. 于是有
可以忽略, 对应着电子的无规则相位最强. 这是近似成立的条件.
可以看出, 两个表达式的关系为 考虑两个函数的比值, 有 上式在高密度极限下远小于 1. 于是有
可以忽略, 对应着电子的无规则相位最强. 这是近似成立的条件.
练习. 计算下面两个动量空间费曼图, 要求对所有内部自旋求和,
所有内部频率积分.
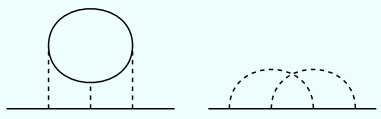 013
013
(第三章完.)

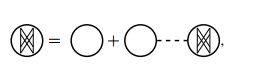




 和
和  的贡献.
的贡献.

