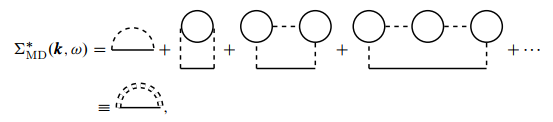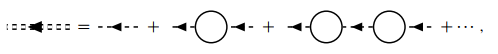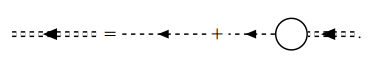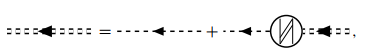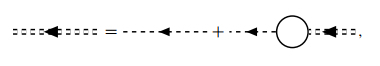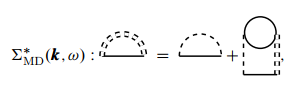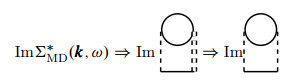零温单粒子格林函数,
费曼图技术及其应用
费曼图技术在凝胶模型中的应用
凝胶模型的哈密顿量是 其中库伦相互作用的形式为 两体相互作用可以用费曼图表示为
 001
001
正规自能骨架图写成
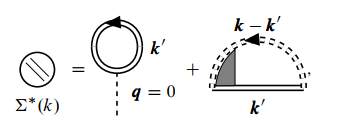 002
002
但由于凝胶模型的哈密顿量中不包含 一项,
所以只有后一个骨架图.
处理凝胶模型时常用的近似有 Hatree-Fock 近似(HFA)和无规相近似(Random
Phase Approximation, RPA), 下面逐一介绍.
Hatree-Fock 近似
Hatree-Fock 近似将骨架图处理为:
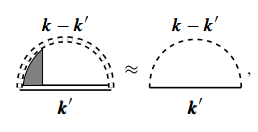 003
003
对应的自能函数表示为 采用球极坐标, 并取极轴沿 方向, 即
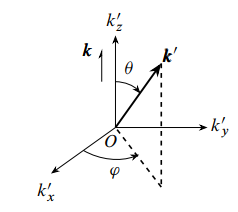 004
004
正规自能可以进一步写成 得到 HF 近似的正规自能: 此时只取了正规自能最简单的形式, 得到的结果不依赖于 , 且当 时,
的一阶导将发散. 由于 没有虚部,
所以格林函数的无穷小虚部不能略去, 即有 上式的极点方程是 其中给定了
值. 将
带入, 其中实部描述准粒子的能量, 虚部描述准粒子的寿命.
并分别令实部和虚部等于零, 得到 但考虑到准粒子的寿命 是无穷大,
这是一个不自然的结果.
下面再来考虑 HF 近似后的定容比热.
设准粒子的有效质量是 , 当温度不高时,
自由粒子的能量可以在费米面附近展开, 有 从而定义准粒子有效质量 在费米面附近将有
以及 .
因此将有比热趋于零, 电导趋于无穷大, 这与金属的实际情况不符.
造成这一结论的原因是 HF 近似忽略了电子间的运动关联, 没有考虑屏蔽效应.
为了进一步修正, 下面继续考虑自能图的各阶修正, 从而引入无规相近似.
无规相(最强发散项)近似
二阶正规自能图有六个, 分别是
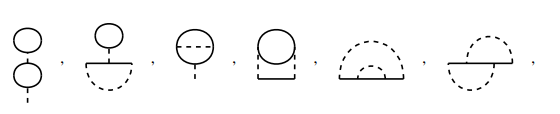 005
005
其中前三项存在 , 不考虑贡献.
第四项正规自能本身存在红外发散, 第五项和第六项正规自能不发散.
记红外发散图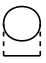 为
,
下面具体分析这一项的贡献.
为
,
下面具体分析这一项的贡献.
正规自能写成
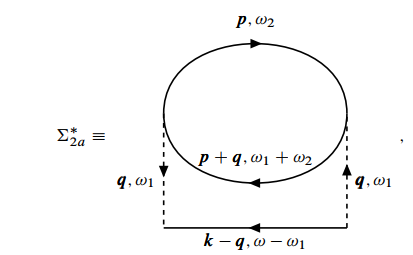 007
007
其中由于有两条相互作用线 , 因此积分 将要发散.
下面具体考虑计算. 按图写出正规自能的表达式: 先对 积分: 被积函数一共有四项相乘, 只有当一个极点在上, 一个极点在下时,
乘积不为零. 由于每一项都以 的形式在无穷远处趋于零,
因此积分可以加上一个半弧形成回路. 此处取上半回路
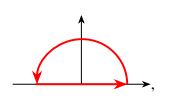 008
008
并利用留数定理, 积分变成 将这一结果代回到 中,
得到 首先完成对
的积分, 先计算 同理可得另一项 代回到原式 中,
得到 作变量代换, 取 , , 表达式变成 然后对
积分, 改写成 下面讨论这一结果的实部. 讨论取 极限后, 的发散行为:
分别计算其中两项与 有关的积分,
选取如下球极坐标:
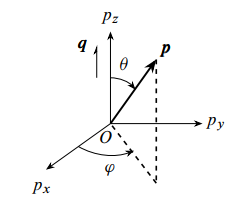 009
009
积分可以进一步写成 其中径向分量在 限制下求积分. 由于 约束条件也就变成 . 积分就是 然后令 , 有 同理可以得到另一项 代回到自能实部
中, 得到 即自能实部以对数形式发散.
下面继续分析更高阶正规自能修正,
寻找规律并利用重整化方法得到合适的结果. 三阶自能图有
 010
010
其中 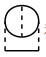 和
和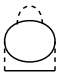 以 形式发散, 而最后一个图
以 形式发散, 而最后一个图
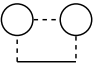 中三条相互作用线具有相同的动量 , 因此发散最强, 以 形式发散.
中三条相互作用线具有相同的动量 , 因此发散最强, 以 形式发散.
类似地, 四阶最强发散项是
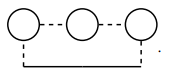 014
014
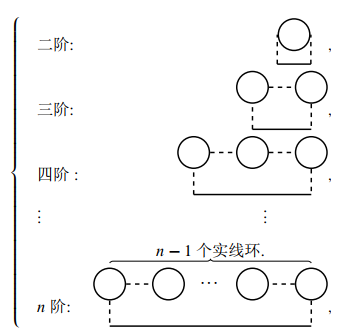
我们考虑的近似方法是, 在每阶近似中只考虑发散最强的项并对它们求和.
各阶最强发散项分别是
 015
015
所有项求和构成不发散的几何级数. 这种处理方法构成凝胶模型的另一个近似,
一般称作最强发散项(Most Divergent, MD)近似,
环图(Ring)近似或无规相(Random Phase, RP)近似.
这种近似下的正规自能处理成如下形式:
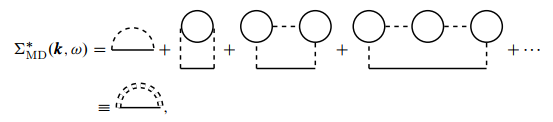 016
016
其中双点线是有效相互作用 ,
在最强发散项近似下取为
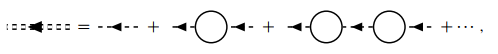 017
017
也就是满足迭代方程
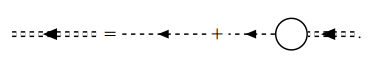 018
018
对比严格的双点线
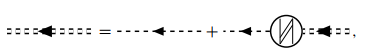 019
019
其中正规自能展开为
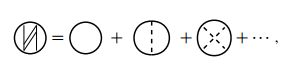 020
020
可以看出, 最强发散项近似下的双点线是对严格双点线的一种近似.
与严格的正规自能相比, 有
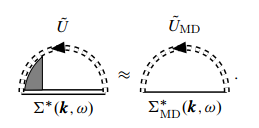 021
021
令:
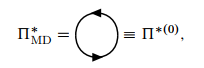 022
022
得到相互作用势的近似表达式 标记好动量空间下的费曼图:
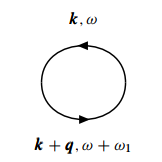 023
023
写出正规极化的表达式: 其中最后一步进行了变量代换, 取 , 并令 .
这一结果与自由粒子的密度关联格林函数有类似的形式, 被称为 Lindhard 函数,
也称因果格林函数.
下面用这一近似计算准粒子的寿命和能谱. 格林函数 极点方程是 其中给定了
值. 先写出形式解: 其中 对应准粒子能谱,
对应准粒子寿命. 设 , 下面推导验证这一假设自洽.
近似后的格林函数是 极点方程是 时, 有 令实部和虚部分别相等, 有 直接给出色散关系的计算结果(D. Pines, Many-Body Problem, 1967):
以及有效质量 这里将粒子所占空间用等体积球表示, 则 的定义是 其中
是玻尔半径,
是每个粒子的平均半径,
是表征粒子半径的量子数.
下面考虑准粒子的寿命, 即正规自能的虚部. 利用关系式
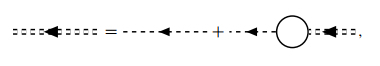 024
024
正规自能图可以重新表示为
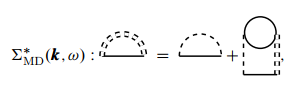 025
025
为简单起见, 虚部取为
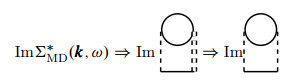 026
026
二阶近似后的实部发散, 但虚部不发散, 用单线计算时结果仅差一常数.
前面已经得到正规自能的表达式 其中, 记第一项积分为 , 第二项积分为 . 第二项的虚部是: 其中, 作变量代换, 令 ,
,
则有 ,
代回表达式中, 有 再令 ,
,
,
由于阶跃函数的限制, 应有 成立. 再取 , 有 其中, 三项对动量的积分分别可以写成 其中, 是立体角,
这里只考虑费米面附近的电子, 可以用费米面上的电子态密度 代表各电子态密度. 等式变成 类似地可以得到 于是得到总的正规自能虚部是 其中 是一个与 有关的常数, 且 . 根据表达式可以看出,
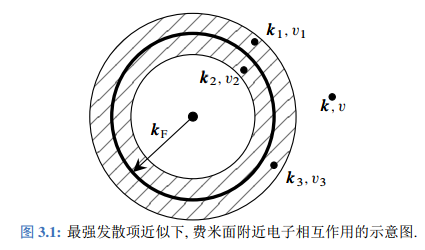
距离费米面越近, 粒子的寿命越长. 这一结果的物理图像如图所示.
可以认为有一动量为
的电子, 它可能来自外界, 也可能是费米面上激发得到的. 它与费米面内动量为
的电子发生相互作用, 二者激发到费米面外动量为 和 的能级上.
 027
027
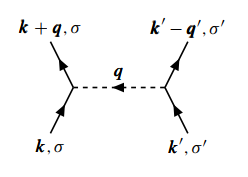
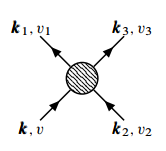
这一过程对应的费曼图是
 028
028
我们考虑的问题是, 是否费米球内的粒子都会和 粒子相互作用,
以及能够发生相互作用的粒子具有什么样的能量. 根据费曼图,
相互作用过程应保持能量守恒, 即 这要求 不能很大,
只有在
窄壳层能的粒子才能产生相互作用. 这一要求对靶粒子和散射态粒子都有限制.
相应的跃迁几率大约是 也就是只有很少的电子能够发生相互作用.
这一结果与费米液体理论得到的结果相同.
下面考虑最强发散项近似下基态电子的分布函数. 自由系统中的粒子分布是
其中自由粒子的基态波函数是 对应的无相互作用的基态粒子分布函数应为一阶跃函数.
而我们所讨论的单粒子格林函数的表达式为 其中: 其中时间变量取为 , 于是 从而可以利用格林函数计算基态粒子分布, 即 格林函数转到频率表象下是 分为以下两种情况考虑.
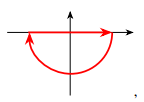
(i)
极点在下半平面, 增加下半平面圆弧构成围道积分, 即
 029
029
于是有
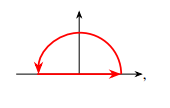
(ii)
极点在上半平面, 增加上半平面圆弧构成围道积分, 有
 030
030
于是有 综上, 有 取 , 有 相应地有分布函数
是一阶跃函数, 所以这一结果是正确的.
下面将以上得到的结果带入最强发散项近似中, 整理. 其中
是极点附近的格林函数: 其中, 称为重整化因子, 是一个与 有关的平滑缓变函数, 并且
. 以及有: 其中最后一步取 .
格林函数可以表示为: 即任意函数可以展开为极点处的平滑函数和其他连续部分之和.
与自由粒子情况类似, 有
有下面两种情况.
(i) , 极点在下半平面,
增加下半平面圆弧构成围道积分, 即
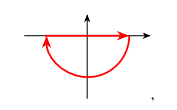 031
031
于是有 其中第二步取 .
(ii) ,
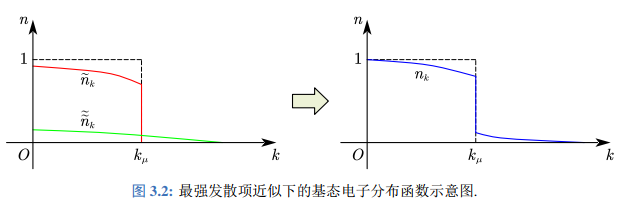
此时取上半平面围道积分, 有 综上, 如果令 为一负小量 , 有 带入粒子分布函数表达式中, 有 以及考虑到相互作用对分布函数有一修正, 得到 这一分布函数对应的图像如图 所示, 函数在费米面处有跳跃,
但不是阶跃函数.
 032
032
凝胶模型的最强发散项近似能够反映系统的等离振荡.
但进一步考虑该模型电子关联, 需要利用密度关联格林函数,
得到介电函数的零点, 即格林函数的极点.
下面利用费曼图对这一方法进行讨论.


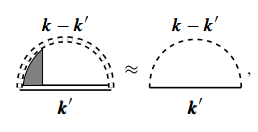


 为
为




 和
和 以
以  中三条相互作用线具有相同的动量
中三条相互作用线具有相同的动量