量子多体理论-第三章(三)
零温单粒子格林函数, 费曼图技术及其应用
坐标空间单粒子格林函数的费曼图技术
费曼图的基本概念
前面得到了零温单粒子格林函数在相互作用绘景下的表达式:
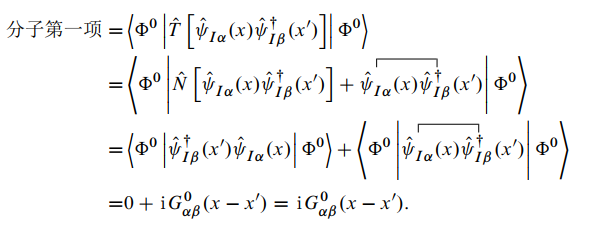
同样可以得到分子的第二项为:
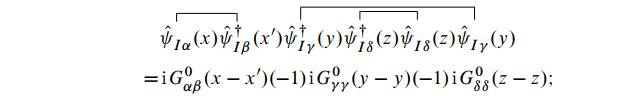
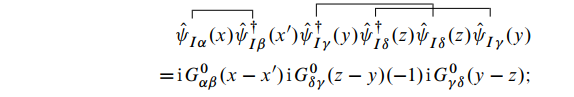
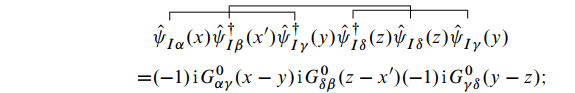
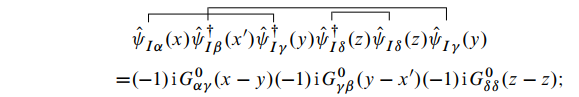
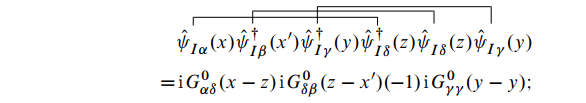
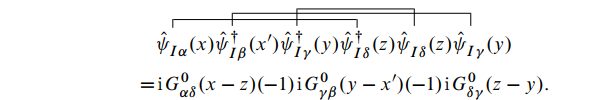
这里需要注意收缩的顺序, 如果顺序交换将产生负号. 另外,
算符收缩后就是一个数, 在计算多个收缩时需要注意不重复交换.
这样分子第二项的贡献可以写为:
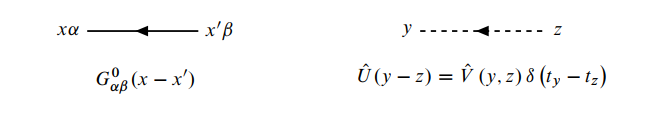
注意这里费曼图中的方向, 表示格林函数
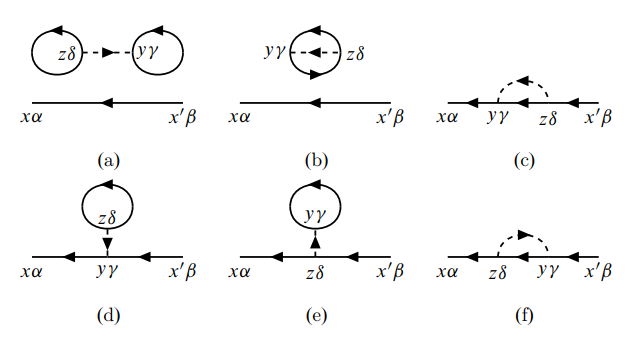
下面借用这6个费曼图, 我们介绍一些基本概念:
1. 相连图和非相连图
可以看到分子一阶展开得到的费曼图中(a)(b)分成两个部分, 彼此不相连,
而费曼图(c)(d)(e)(f)彼此相连.
像(c)(d)(e)(f)这样所有坐标点通过实线或点线与外线相连的图叫做连接图.
这里的外线是与点
2. 真空涨落图和传播图
费曼图(a)(b)中的圈图 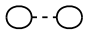 和
和  最终积分后将得到常数, 只留下自由传播子,
这样的图也称为真空涨落图.
与之对应的是传播图, 即存在与外点相连内点的图,
如(c)(d)(e)(f).
最终积分后将得到常数, 只留下自由传播子,
这样的图也称为真空涨落图.
与之对应的是传播图, 即存在与外点相连内点的图,
如(c)(d)(e)(f).
下面说明非连接图对格林函数没有贡献. 格林函数的分子部分可以用费曼图写为:
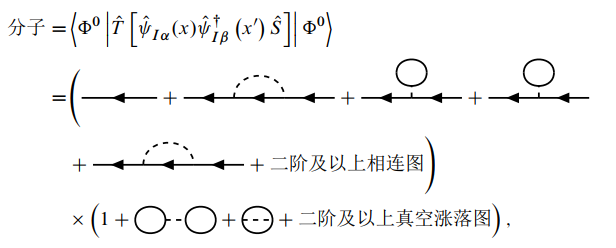
而分母部分可以写为:
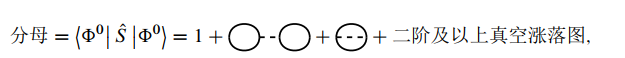
则:
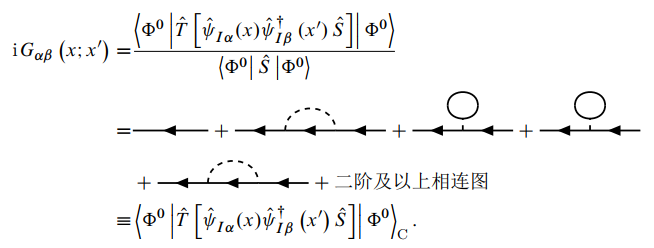
这里的 C 是 Connected, 即相连的意思. 可以看到, 在计算格林函数时, 分子分母中不相连的真空涨落图相消, 只留下相连图.
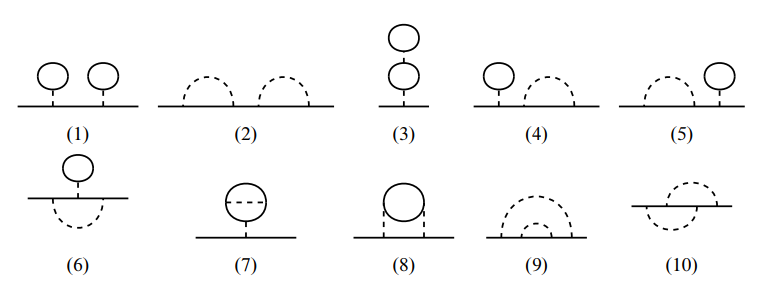
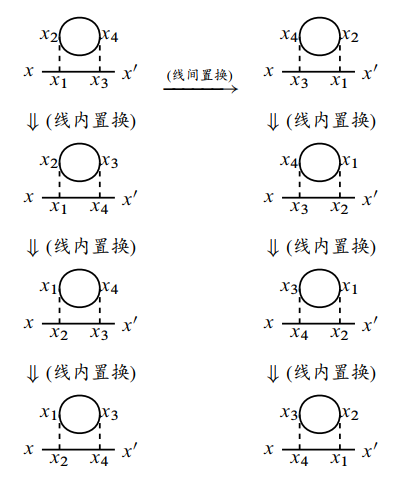
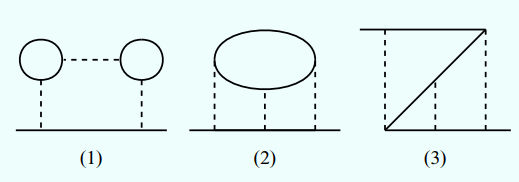
二阶拓扑不等价相连图一共有十个, 分别是:
坐标空间的费曼图规则
下面对坐标空间中
(i)画出所有含
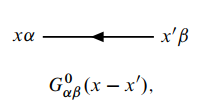
点线对应
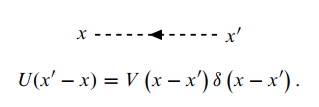
(ii)对所有内部时空变量积分,对所有内部自旋变量求和.
(iii)所得结果前乘因子
(iv)规定
这里
前面考虑的是
格林函数的
综上, 总系数是
处理如下费曼图内部自旋变量:
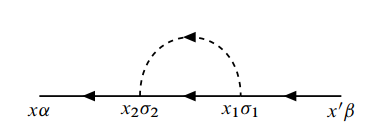
图中没有闭合实线环,有一条点线. 按费曼图规则得到
计算如下一阶图形:
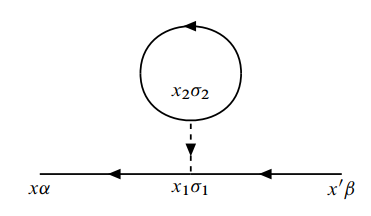
图中有一个实线环, 一条点线, 故有:
在实际进一步计算过程中, 对实空间积分的计算过于繁琐, 因此下面考虑傅立叶变换到动量空间中的费曼图技术.
练习. 计算十个二阶拓扑不等价相连图, 只要求完成对内部自旋变量求和.
动量空间单粒子格林函数的费曼图技术
傅立叶变换
定义四维坐标:
当
动量空间
(i) 画出所有含
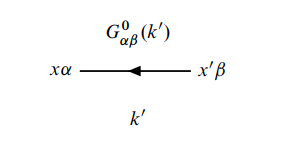
点线对应
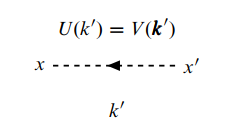
两条外线对应着
(ii) 对每一个顶点, 四维动量保持守恒, 如下图所示.
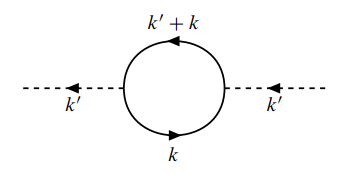
(iii) 对所有内部动量积分, 对所有内部自旋求和.
(iv) 所得结果前乘上因子
(v) 形成闭合环的
下面按照这些规则, 重新写出前一节给出的两种费曼图.
(a)
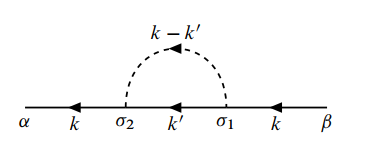
(b)
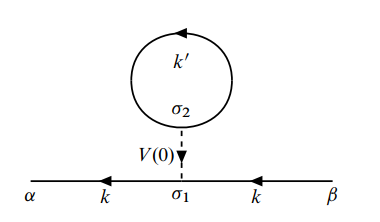
练习. 按费曼图规则写出下列动量空间费曼图各顶点和线的标记, 并对自旋求和.
Dyson 方程
坐标空间中的 Dyson 方程
坐标空间中的全格林函数写作
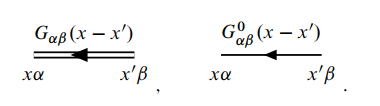
于是全格林函数的展开式可以用费曼图表示为
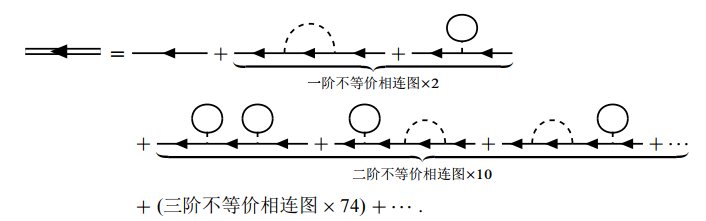
上式的等价形式是
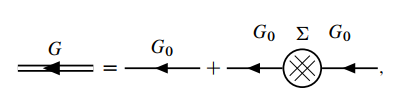
其中, 称 为自能(self energy), 记作
为自能(self energy), 记作
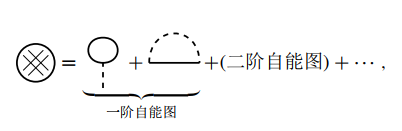
其中十个二阶自能图的具体形式为
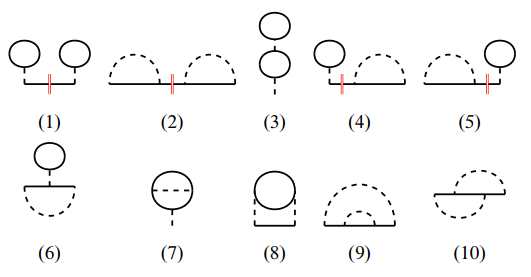
如图所示, 第 1, 2, 4, 5 个二阶自能图可以通过断开一条
正规自能图 若一个自能图不能通过断开一条
线而分成两部分, 则称其为正规自能图 , 记作 展开式为:
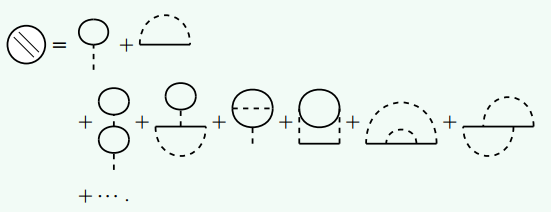
自能图  可以用正规自能
可以用正规自能  表示, 即
表示, 即
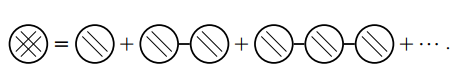
于是全格林函数可以表示成
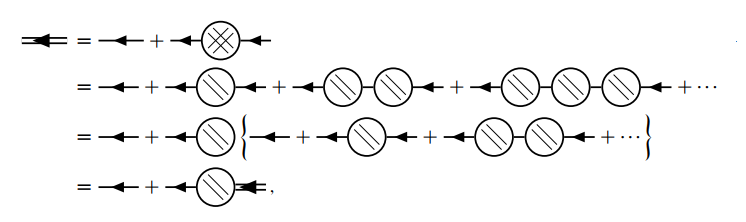
这样就得到了 Dyson 方程的另一种形式:
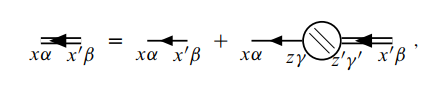
对应的数学表达式为
动量空间中的 Dyson 方程
格林函数, 相互作用势和正规自能的傅里叶变换表达式分别为
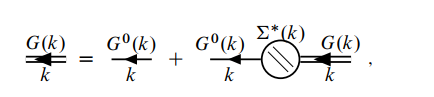
从中可以解出
正规自能骨架图
Dyson 方程中的正规自能本身同样很复杂, 为方便后续处理, 将它拆分为两部分:
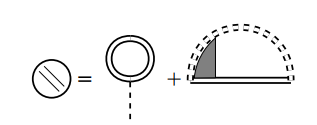
下面具体分析其中每一部分.
(a) 对粒子线的修正.
对粒子线的修正有如下两部分.
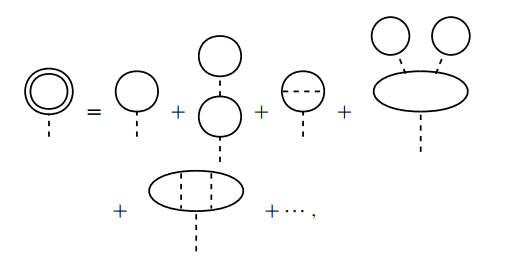
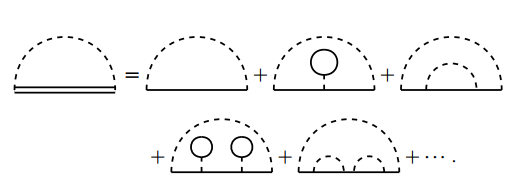
(b) 对相互作用线的修正.
相互作用

(c) 顶角修正.
剩余不能归为粒子线修正或相互作用线修正的项, 统称为顶角修正. 有:
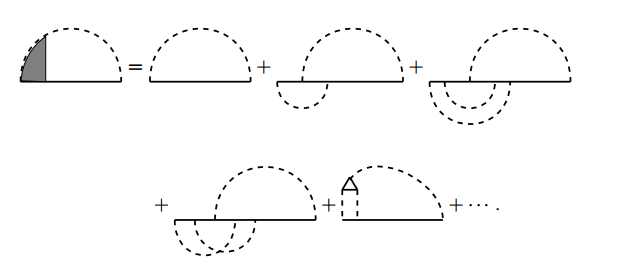
极化图
进一步讨论相互作用线, 首先可以把它写成
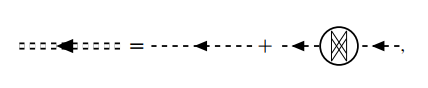
其中,  称为极化图, 记作
称为极化图, 记作
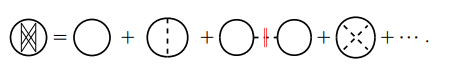
与前面对正规自能图的定义类似, 可以将极化图分成正规极化图和非正规极化图.
正规极化图 不能通过断开一条相互作用线而分成两部分的极化图称为正规极化图
, 费曼图记作
极化图用正规极化图表示为
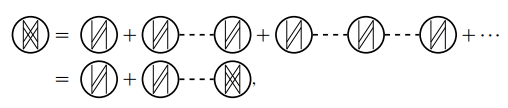
对应的方程为
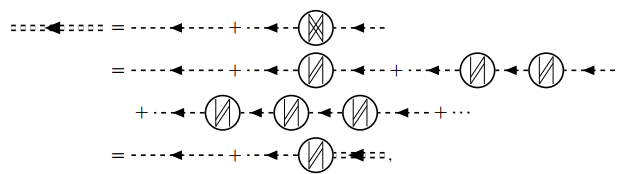
从中可以解出
