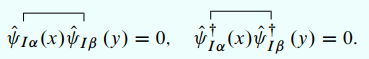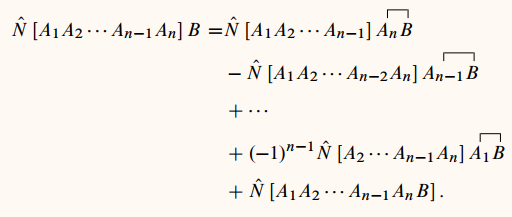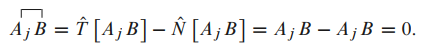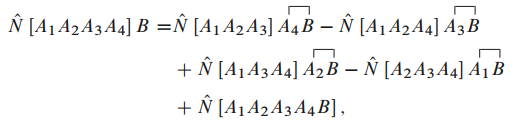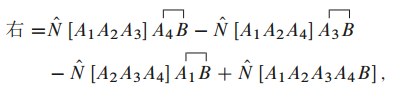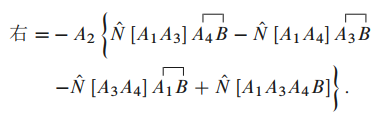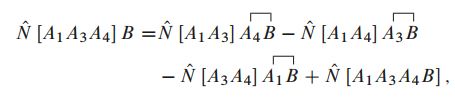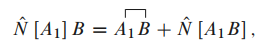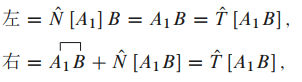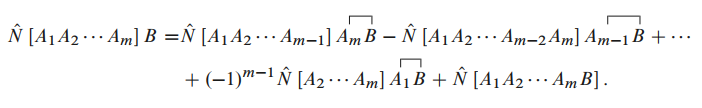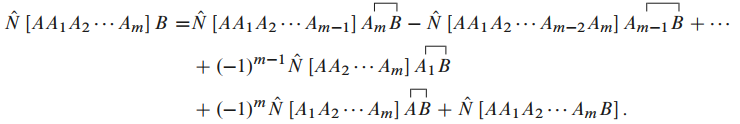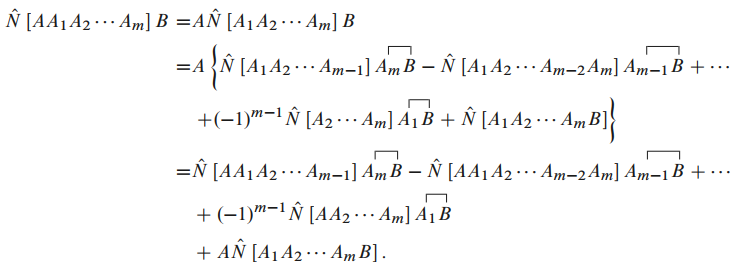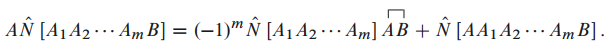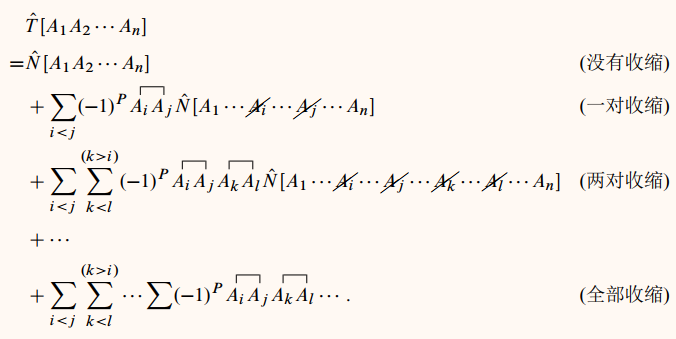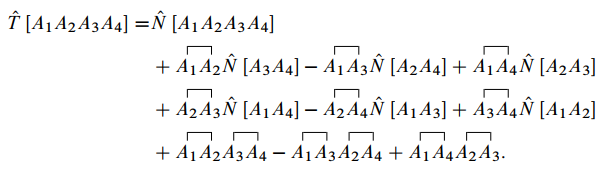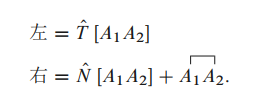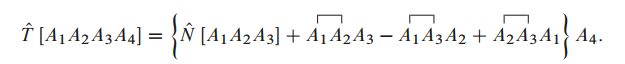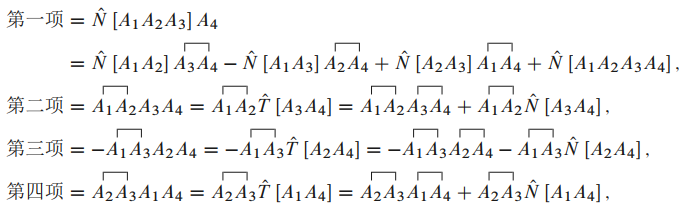系列笔记同步发布在佩璇的公众号🐕佩璇小窝中,
欢迎关注.
零温单粒子格林函数,
费曼图技术及其应用
单粒子格林函数的相互作用绘景
首先回顾一下已知的内容. 单粒子格林函数定义为 其中 是系统的基态, 满足 考虑哈密顿量
可以写为不包含相互作用的
和包含相互作用的 两项: 其中 相对于 是小量, 有 其中
对应自由粒子系统的基态能,
是无相互作用哈密顿量的基态.
这些结果都是在海森堡绘景下得到的, 在微扰论的框架下计算时,
需要考虑到无穷阶修正. 为此, 需要使用费曼图技术来计算格林函数,
下面引入相互作用绘景中的格林函数.
变换关系
设相互作用绘景中的时间演化算符为 , 满足以下变换关系: 则相互作用绘景和海森伯绘景中算符间的变换关系为: 同样可以得到态矢量间的关系: 特别地, 取 , 有:
相互作用的绝热引入()
前面我们获得了海森伯绘景与相互作用绘景中算符和态矢量间的关系.
考虑系统总的
可以表示为不含时的可解哈密顿量 和微扰 的求和, 一般情况下有: 接下来, 尝试用 的基态 表示 的基态 .
为此引入如下含有参数的随时间变化的哈密顿量: 其中 是一个正的小量, 在特殊的时间点有:
可以看出当 足够小时,
随时间的演化将十分缓慢, 相当于是一个绝热过程. 利用量子力学的绝热定理:
假设体系哈密顿量由
绝热演化到 ,
如果量子客体开始处于
的第 个本征态, 它将演化至 的第
个本征态(假定演化过程中谱是分立的并且不简并, 即态的次序不会混淆).
这里考虑哈密顿量为 的体系从 时的基态 开始绝热演化,
所以体系将一直处于各个时期哈密顿量的基态. 假设 时就会演化到实际哈密顿量的基态 . 在 时有本征方程: 在薛定谔绘景下的态矢量
满足薛定谔方程: 因为
是不含时的, 所以对于 , 近似有: 由相互作用绘景中态矢量和薛定谔绘景中态矢量间的关系, 有: 注意现在考虑的是 的情况, 有: 利用相互作用绘景中态矢量的演化式, 可以得到 时的态矢量: 利用海森伯绘景中态矢量与相互作用绘景中态矢量间的关系可以得到:
此即实际哈密顿量的基态 与已知的
间的关系.
同样地, 可以令哈密顿量从
绝热演化到 ,
这样基态
可以演化到 ,
这时两者可能相差一个相位.
利用相互作用绘景中态矢量的与薛定谔绘景中态矢量的关系, 可以得到
时相互作用绘景中的态矢量: 这里 是可能的相位差.
利用相互作用绘景中态矢量的演化式, 可以得到 时的态矢量: 这样我们就得到了 与
间的另一关系式. 定义 的左矢,
取上式的厄米共轭得到:
由
归一, 得到: 𝟙 定义 为散射算符, 可以得到:
前面得到了 和 的关系,
下面利用这一关系将海森伯绘景下的格林函数转化为相互作用绘景下的格林函数.
为此, 需要计算 .
首先计算 的情况:
考虑到时间演化算符具有哈密顿量的 e 指数形式, 由于 中只有费米子算符的偶数次项乘积(
为二次项, 为四次项), 因此算符 或
在时序乘积下对换不会有符号问题. 故 可以证明当 时, 结果同上. 故有: 取,
则可以得到零温单粒子格林函数在相互作用绘景下的表示:
Wick 定理
本节的讨论都是对于费米子体系而言的.
由量子力学知识, 可以得到散射算符 的表示: 其中 . 对于两体相互作用有: 故 引入含时的二体相互作用: 可知 与 有如下关系: 则两体相互作用可重新表示为: 进一步对时间进行积分可以得到: 上式就是散射矩阵
展开后的一阶项, 可以看出共有四个场算符.
引入四维坐标, 令 , 则 格林函数式可写为 上式分子可以展开为:
可以看出格林函数的分子展开后将总是偶数个场算符编时乘积的基态平均.
对于第二项, 有
正规乘积
为计算编时乘积我们引入正规乘积.
为此先把场算符分解为"产生"算符和"消灭"算符之和.
这里的"产生"算符和"消灭"算符是定义在自由粒子体系的基态 上的,
而不是定义在真空态 上,
具体有:
若 ,
则称 为"消灭"算符;
若 , 则称
为"产生"算符.
考虑自由费米子体系, 对于真空态的产生和消灭算符为 和 , 体系基态为: 分两种情况考虑:
:
, 此时 是"消灭"算符.
, 此时 是"产生"算符.
:
, 此时 是"产生"算符.
, 此时 是"消灭"算符.
通常
可以写为二次量子化的形式: 对于相互作用绘景下的场算符进行平面波展开, 可以得到: 对于费米子体系, 场算符可以分成如下"消灭"算符和"产生"算符的和:
其中定义了 同样, 可以得到: 其中 可证 、 是"消灭"算符, 、 是
"产生" 算符, 满足如下关系:
正规乘积是指将所有"产生"算符排在所有"消灭"算符左边的表示, 用 表示. 例如有如下的正规乘积: 对于费米型算符 , 正规乘积具有性质: 其中
表示算符乘积一组排列,
是初始的排列变为正规乘积所需要进行的对换数, 例如: 特别地, 对于两个和三个算符的正规乘积有: 当 为"消灭"算符时, 有
当 为"产生"算符时, 有
两个算符的收缩
为计算编时乘积,
我们引入两个算符间的收缩(contraction):
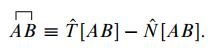 001
001
收缩的性质:
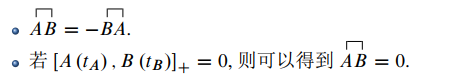 002
002
Proof. 由于 所以 又
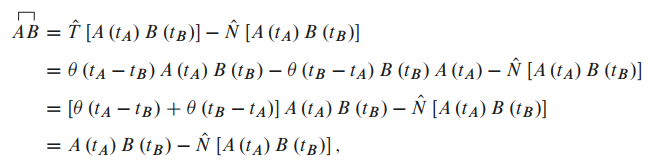 003
003
注意到 若是产生算符若是消灭算符
则证得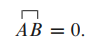
推论:
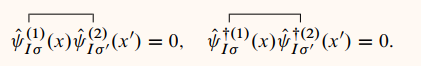 005
005
Proof. 考虑到收缩的性质, 可以计算算符间的反对易关系,
如果结果为零, 则推论成立. 将 、、 和
的表达式代入到反对易式中得到: 同样, 有:
这样就验证了费米子体系的"产生"算符间的收缩和"消灭"算符间的收缩都为零.
◻
下面计算两个场算符的收缩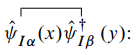
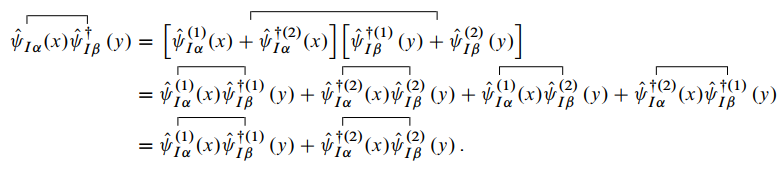 007
007
分别计算这两项. 对第一项:
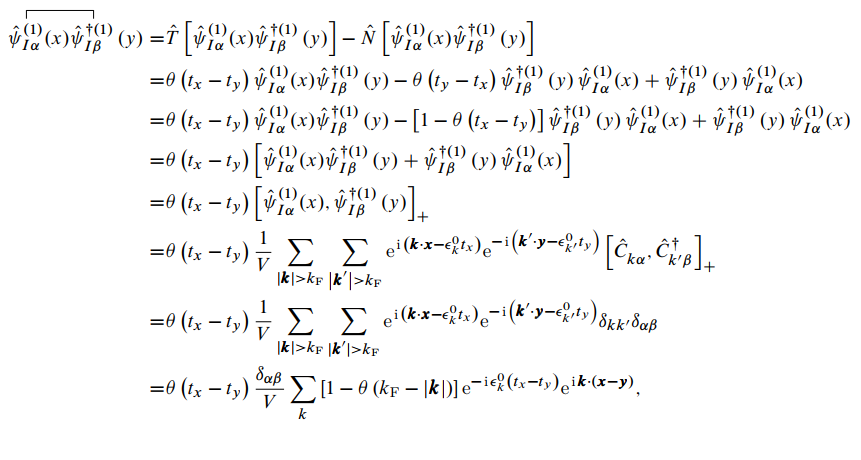 008
008
类似可求得第二项:
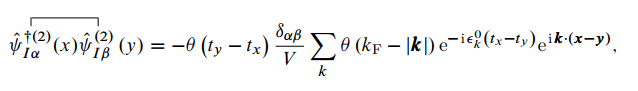 009
009
故
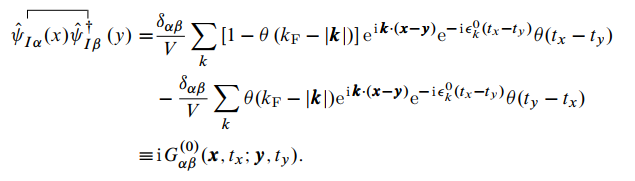 010
010
这个结果正是前面得到的自由费米子体系零温格林函数表达式, 为一常数.
同样地,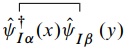 亦为一常数.
亦为一常数.
练习. 证明:
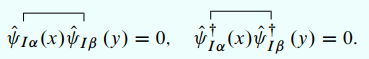 012
012
辅助定理
证明 Wick 定理之前, 先引入辅助定理:
辅助定理 设有一组(个)海森伯绘景中的"产生"和"消灭"算符:
,
其中算符
的时刻比其它算符的时刻都小, 即 .
有如下关系:
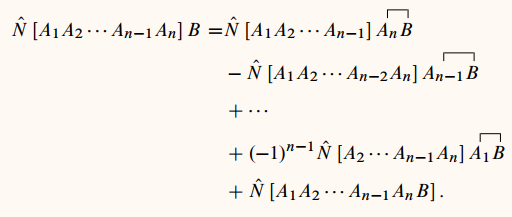 013
013
下面分两种情况证明辅助定理.
Proof. (1)
为"消灭"算符
这时任意的 与 的正规乘积为: 考虑到 的时间比 小, 可以得到两者的收缩为:
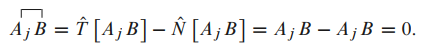 014
014
上面结果代回到辅助定理(3.8.36)中我们得到: 右左 辅助定理成立.
(2) 为"产生"算符
这时可以只考虑 是"消灭"算符的情况. 下面以 的情况对这一点进行说明, 并假设 是"产生"算符, 其余为"消灭"算符.
当 时,
要证明的辅助定理为
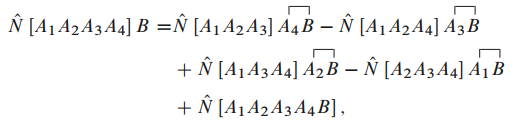 015
015
注意"产生"算符与"产生"算符之间的收缩为0, 则
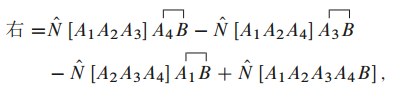 016
016
利用正规乘积的性质, 有
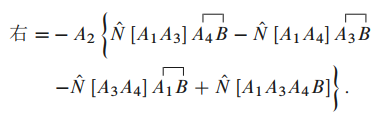 017
017
同样地, 对左边, 有 左 比较上两式, 可以发现我们只需要证明
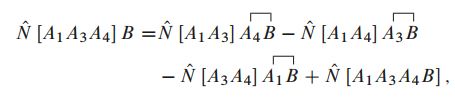 018
018
即不需要考虑"产生"算符.
下面用数学归纳法进行证明.
首先验证 时定理成立. 时定理为
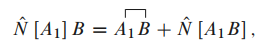 019
019
利用收缩的定义式, 有
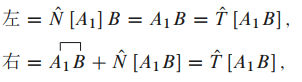 020
020
即 时辅助定理是成立的.
下面假设
时辅助定理成立, 即有如下等式:
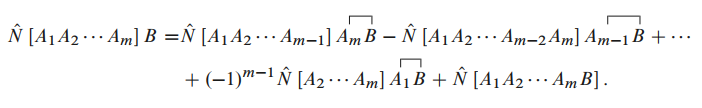 021
021
接下来用这一关系证明
时的辅助定理, 即要证明:
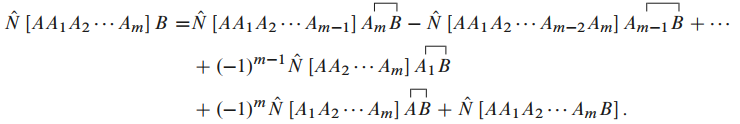 022
022
由于
均为"消灭"算符, 正规乘积里没有"产生"算符时可以提到括号外, 故可以利用
时的公式可以计算上式左边:
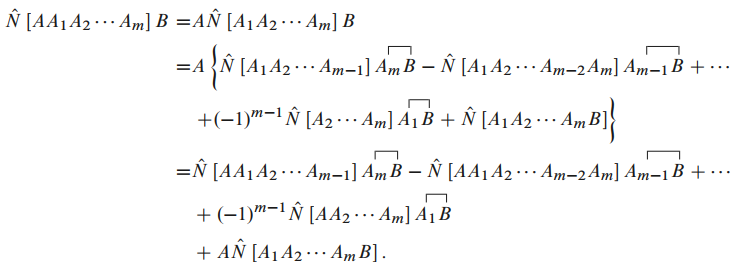 023
023
对比要证明的式子, 我们只需证明:
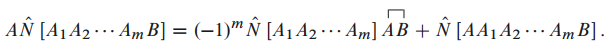 024
024
可以直接从左边证明: 
这样就证明了
是"产生"算符时的辅助定理.
综上, 辅助定理成立. ◻
Wick定理
Wick定理 一组费米子"产生"和"消灭"算符
的编时乘积可以表示为对其中若干对算符取收缩,
而其余算符取正规乘积的所有可能取值之和:
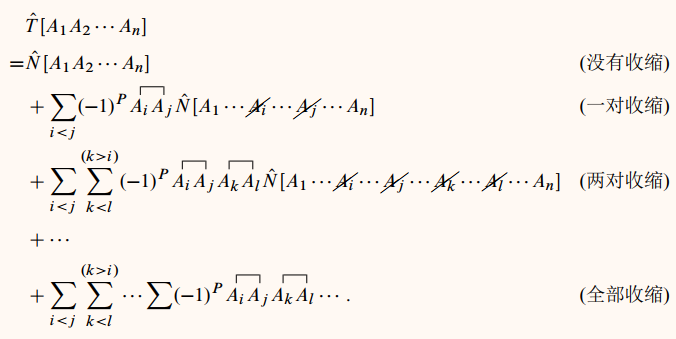 026
026
这里每一项中的
是计算缩并的时候, 算符交换的次数,
统一用一个符号表示(可以推广到玻色子情况, 就没有这一系数了).
这里的全部收缩项中, 如果是偶数个算符的编时乘积, 就得到一个数;
如果是奇数个算符, 则全部收缩项是单个"产生"算符和"消灭"算符的线性组合.
通常用到的编时乘积只涉及偶数个算符,
例如前面格林函数中编时乘积的算符就是偶数个的. 或者可以这样考虑,
我们总是要对编时乘积计算基态平均,
奇数个"产生"和"消灭"算符的基态平均总是零.
时的 Wick 定理:
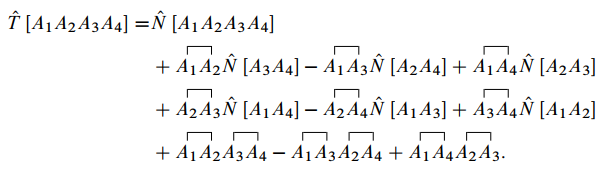 029
029
下面用数学归纳法证明 Wick 定理.
Proof. 验证初始
时的 Wick 定理:
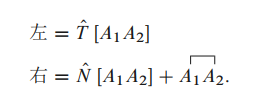 030
030
可以看出这时的 Wick 定理就是收缩的定义式, 所以 时, Wick 定理是成立的.
按照数学归纳法的步骤, 应该假设 时的 Wick 定理成立, 以此证明 时的 Wick 定理成立. 为了简单明了,
我们展示以下步骤: 假设
时的Wick定理成立来验证
的Wick定理. 这与假设
时的Wick定理成立来验证
的Wick定理步骤类似. 假设 ,
有: 假设 时成立, 有:
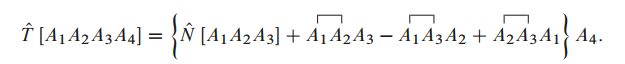 027
027
利用辅助定理可以分别得到右边每一项为:
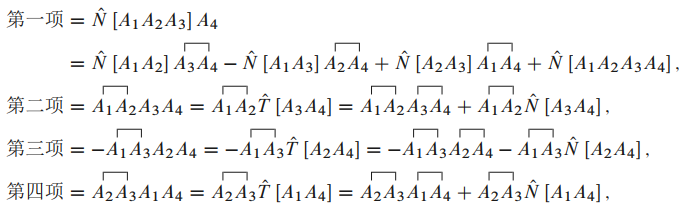 028
028
合起来则得到 的 Wick 定理.
◻
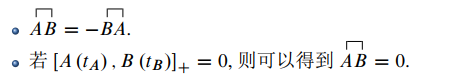
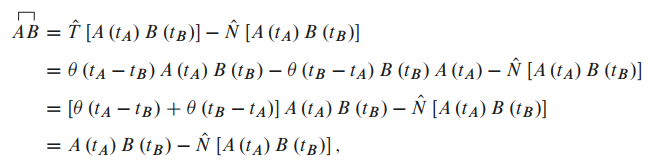
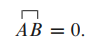
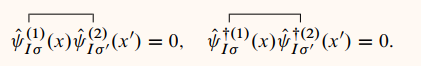
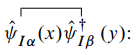
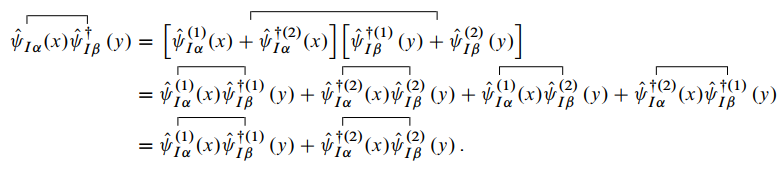
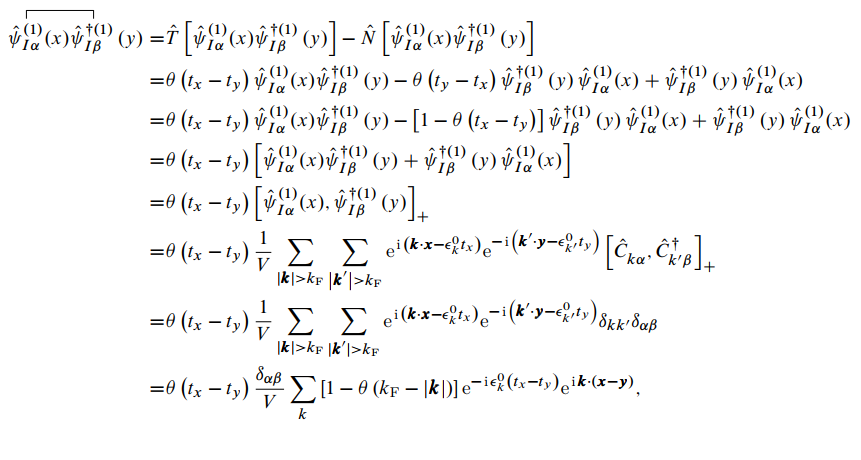
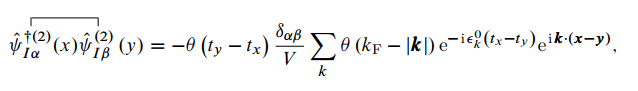
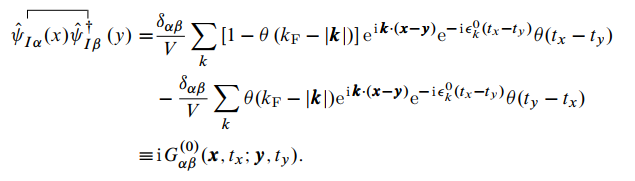
 亦为一常数.
亦为一常数.